Measuring the Clustering Performance (Silhouette Analysis)

The real world data is not naturally organized into number of distinctive clusters. Due to this reason, it is not easy to visualize and draw inferences. That is why we need to measure the clustering performance as well as its quality. It can be done with the help of silhouette analysis.

Silhouette Analysis

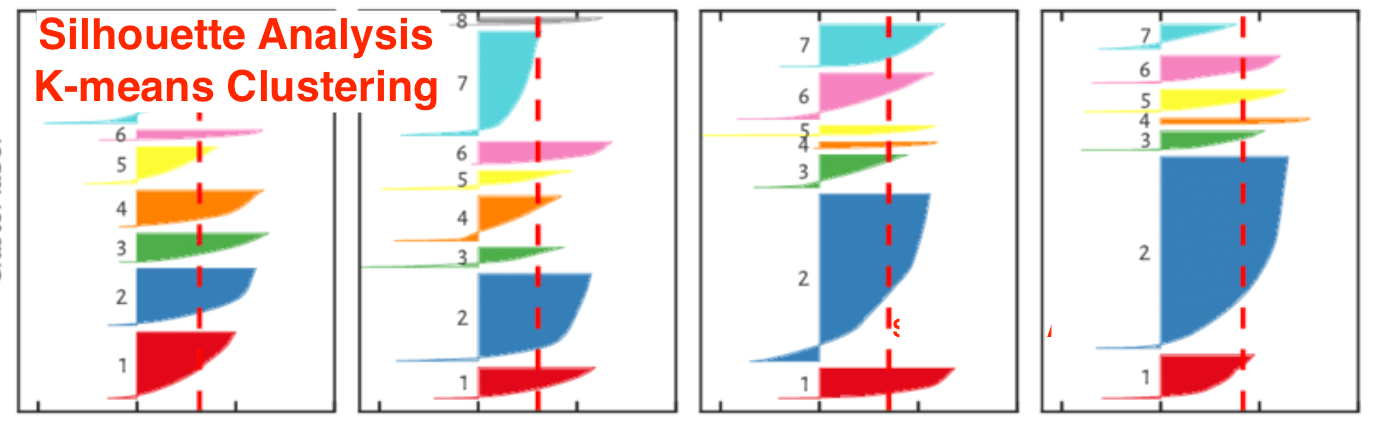
This method can be used to check the quality of clustering by measuring the distance between the clusters. Basically, it provides a way to assess the parameters like number of clusters by giving a silhouette score. This score is a metric that measures how close each point in one cluster is to the points in the neighboring clusters.

Analysis of silhouette score

The score has a range of [-1, 1]. Following is the analysis of this score:
Score of +1: Score near +1 indicates that the sample is far away from the neighboring cluster.
Score of 0: Score 0 indicates that the sample is on or very close to the decision boundary between two neighboring clusters.

Score of -1: Negative score indicates that the samples have been assigned to the wrong clusters.

Lets learn how to calculate the silhouette score.

Silhouette score can be calculated by using the following formula:

𝑠𝑖𝑙ℎ𝑜𝑢𝑒𝑡𝑡𝑒 𝑠𝑐𝑜𝑟𝑒=(𝑝−𝑞)/max (𝑝,𝑞)

Here, 𝑝 is the mean distance to the points in the nearest cluster that the data point is not a part of. And, 𝑞 is the mean intra-cluster distance to all the points in its own cluster.

For finding the optimal number of clusters, we need to run the clustering algorithm again by importing the metrics module from the sklearn package. In the following example, we will run the K-means clustering algorithm to find the optimal number of clusters:

Import the necessary packages as shown:
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

With the help of the following code, we will generate the two-dimensional dataset, containing four blobs, by using make_blob from the sklearn.dataset package.

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=500, centers=4,
cluster_std=0.40, random_state=0)
Initialize the variables as shown:
scores = []
values = np.arange(2, 10)

We need to iterate the K-means model through all the values and also need to train it with the input data.

for num_clusters in values:
kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10)
kmeans.fit(X)

Now, estimate the silhouette score for the current clustering model using the Euclidean distance metric:

score = metrics.silhouette_score(X, kmeans.labels_,
metric='euclidean', sample_size=len(X))

The following line of code will help in displaying the number of clusters as well as Silhouette score.

print("\nNumber of clusters =", num_clusters)
print("Silhouette score =", score)
scores.append(score)

You will receive the following output:

Number of clusters = 9
Silhouette score = 0.340391138371
num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

Now, the output for optimal number of clusters would be as follows:

Optimal number of clusters = 2

In the next post we'll try to understand the concept of finding the nearest neighbors.