The Bayes rule

Now we will discuss one very important formula which can be used to weigh conflicting pieces of evidence in medicine, in a court of law, and in many (if not all) scientific disciplines.The formula is called the Bayes rule (or the Bayes formula). 

We will start by demonstrating the power of the Bayes rule by means of a simple medical diagnosis problem where it highlights how poorly our intuition is suited for combining conflicting evidence. We will then show how the Bayes rule can be used to build AI methods that can cope with conflicting and noisy observations.

Prior and posterior odds

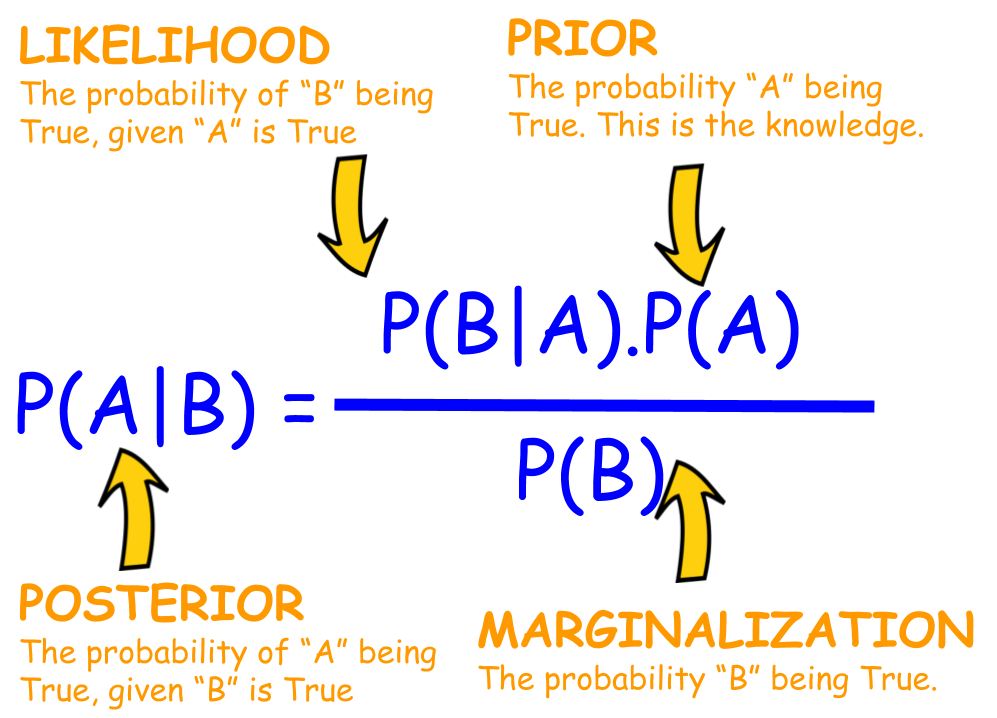
The Bayes rule can be expressed in many forms. The simplest one is in terms of odds. The idea is to take the odds for something happening (against it not happening), which we´ll call prior odds. The word prior refers to our assessment of the odds before obtaining some new information that may be relevant. The purpose of the formula is to update the prior odds when new information becomes available, to obtain the posterior odds, or the odds after obtaining the information (the dictionary meaning of posterior is “something that comes after, later.)”

How odds change

In order to weigh the new information, and decide how the odds change when it becomes available, we need to consider how likely we would be to encounter this information in alternative situations. Let’s take as an example, the odds that it will rain later today. Imagine getting up in the morning in Finland. The chances of rain are 206 in 365 (including rain, snow, and hail. Brrr). The number of days without rain is therefore 159. This converts to prior odds of 206:159 for rain, so the cards are stacked against you already before you open your eyes.

However, after opening your eyes and taking a look outside, you notice it’s cloudy. Suppose the chances of having a cloudy morning on a rainy day are 9 out of 10 – that means that only one out of 10 rainy days start out with blue skies. But sometimes there are also clouds without rain: the chances of having clouds on a rainless day are 1 in 10. Now how much higher are the chances of clouds on a rainy day compared to a rainless day? Think about this carefully as it will be important to be able to comprehend the question and obtain the answer in what follows.

The answer is that the chances of clouds are nine times higher on a rainy day than on a rainless day: on a rainy day the chances are 9 out of 10, whereas on a rainless day the chances of clouds are 1 out of 10, and that makes nine times higher.

Note that even thought the two probabilities 9/10 and 1/10 sum up to 9/10 + 1/10 = 1, this is by no means always the case. In some other town, the mornings of rainy days could be cloudy eight times out of ten. This, however, would not mean that the rainless days are cloudy two times out of ten. You'll have to be careful to get the calculations right. (But never mind if you make a mistake or two – don't give up! The Bayes rule is a fundamental thinking tool for everyone of us.)

Likelihood ratio

The above ratio (nine times higher chance of clouds on a rainy day than on a rainless day) is called the likelihood ratio. More generally, the likelihood ratio is the probability of the observation in case the event of interest (in the above, rain), divided by the probability of the observation in case of no event (in the above, no rain). Please read the previous sentence a few times. It may look a little intimidating, but it´s not impossible to digest if you just focus carefully. We will walk you through the steps in detail, just don´t lose your nerve. We´re almost there.

So we concluded that on a cloudy morning, we have: likelihood ratio = (9/10) / (1/10) = 9

The mighty Bayes rule for converting prior odds into posterior odds is – ta-daa! – as follows: posterior odds = likelihood ratio × prior odds

Now you are probably thinking: Hold on, that’s the formula? It’s a frigging multiplication! That is the formula – we said it’s simple, didn’t we? You wouldn’t imagine that a simple multiplication can be used for all kinds of incredibly useful applications, but it can. We’ll study a couple examples which will demonstrate this.

The Bayes rule in practice: breast cancer screening

Our first realistic application is a classical example of using the Bayes rule, namely medical diagnosis. This example also illustrates a common bias in dealing with uncertain information called the base-rate fallacy.

Consider mammographic screening for breast cancer. Using made up percentages for the sake of simplifying the numbers, let’s assume that 5 in 100 women have breast cancer. Suppose that if a person has breast cancer, then the mammograph test will find it 80 times out of 100. When the test comes out suggesting that breast cancer is present, we say that the result is positive, although of course there is nothing positive about this for the person being tested (a technical way of saying this is that the sensitivity of the test is 80%).

The test may also fail in the other direction, namely to indicate breast cancer when none exists. This is called a false positive finding. Suppose that if the person being tested actually doesn’t have breast cancer, the chances that the test nevertheless comes out positive are 10 in 100. (In technical terms, we would say that the specificity of the test is 90%.)

Based on the above probabilities, you are able to calculate the likelihood ratio. You'll find use for it in the next exercise. If you forgot how the likelihood ratio is calculated, you may wish to check the terminology box earlier in this section and revisit the rain example.

Note: You can use the above diagram with stick figures to validate that your result is in the ballpark (about right) but note that diagram isn't quite precise. Out of the 95 women who don't have cancer (the gray figures in the top panel), about nine and a half are expected to get a (false) positive result. The remaining 84 and a half are expected to get a (true) negative result. We didn't want to be so cruel as to cut people – even stick figures – in half, so we used 10 and 85 as an approximation.