How neural networks are built

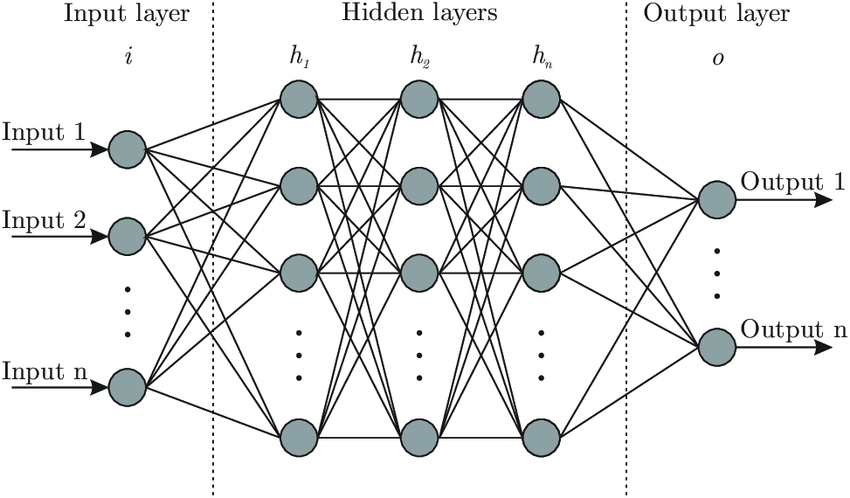
The basic artificial neuron model involves a set of adaptive parameters, called weights like in linear and logistic regression. Just like in regression, these weights are used as multipliers on the inputs of the neuron, which are added up. The sum of the weights times the inputs is called the linear combination of the inputs.

If we have a neuron with six inputs (analogous to the amounts of the six shopping items: potatoes, carrots, and so on), input1, input2, input3, input4, input5, and input6, we also need six weights. The weights are analogous to the prices of the items. We’ll call them weight1, weight2, weight3, weight4, weight5, and weight6. In addition, we’ll usually want to include an intercept term like we did in linear regression. This can be thought of as a fixed additional charge due to processing a credit card payment, for example:

We can then calculate the linear combination like this: linear combination = intercept + weight1 × input1 + ... + weight6 × input6 (where the ... is a shorthand notation meaning that the sum include all the terms from 1 to 6).

With some example numbers we could then get: 

10.0 + 5.4 × 8 + (-10.2) × 5 + (-0.1) × 22 + 101.4 × (-5) + 0.0 × 2 + 12.0 × (-3) = -543.0

The weights are almost always learned from data using the same ideas as in linear or logistic regression, as discussed previously. But before we discuss this in more detail, we’ll introduce another important stage that a neuron completes before it sends out an output signal.

Activations and outputs

Once the linear combination has been computed, the neuron does one more operation. It takes the linear combination and puts it through a so-called activation function. Typical examples of the activation function include:

• identity function: do nothing and just output the linear combination
• step function: if the value of the linear combination is greater than zero, send a pulse (ON), otherwise do nothing (OFF)
• sigmoid function: a “soft” version of the step function

Note that with the first activation function, the identity function, the neuron is exactly the same as linear regression. This is why the identity function is rarely used in neural networks: it leads to nothing new and interesting.

The output of the neuron, determined by the linear combination and the activation function, can be used to extract a prediction or a decision. For example, if the network is designed to identify a stop sign in front of a self-driving car, the input can be the pixels of an image captured by a camera attached in front of the car, and the output can be used to activate a stopping procedure that stops the car before the sign.

Learning or adaptation in the network occurs when the weights are adjusted so as to make the network produce the correct outputs, just like in linear or logistic regression. Many neural networks are very large, and the largest contain hundreds of billions of weights. Optimizing them all can be a daunting task that requires massive amounts of computing power.

How neurons activate

Real, biological neurons communicate by sending out sharp, electrical pulses called “spikes”, so that at any given time, their outgoing signal is either on or off (1 or 0). The step function imitates this behavior. However, artificial neural networks tend to use activation functions that output a continuous numerical activation level at all times, such as the sigmoid function. Thus, to use a somewhat awkward figure of speech, real neurons communicate by something similar to the Morse code, whereas artificial neurons communicate by adjusting the pitch of their voice as if yodeling.