Implementation of solutions using Genetic Algorithms

Generating bit patterns

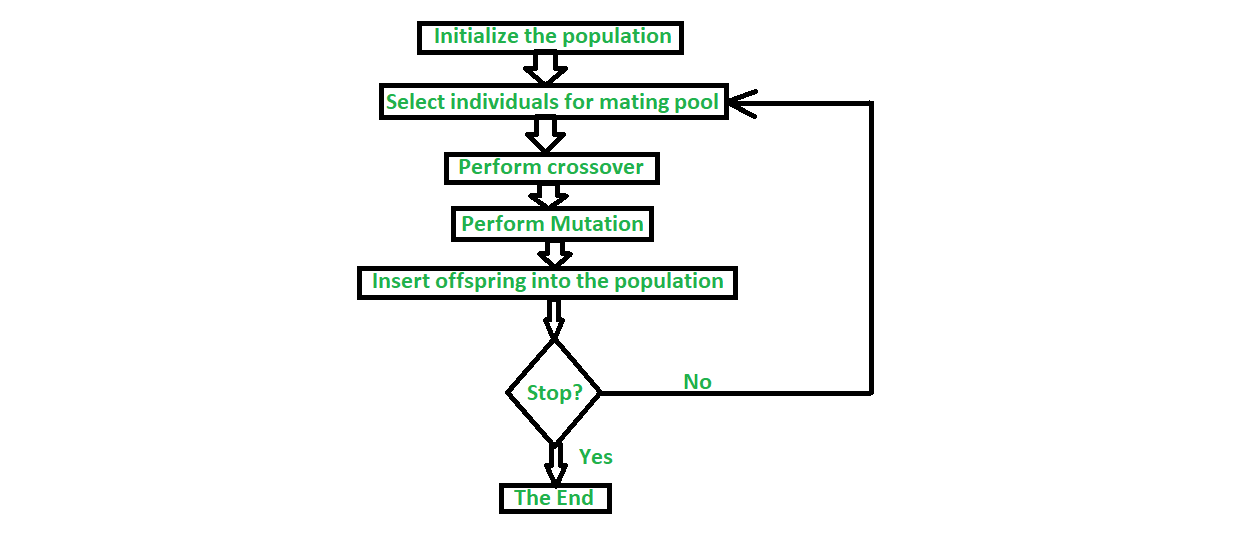
The following example shows you how to generate a bit string that would contain 15 ones, based on the One Max problem.

Import the necessary packages as shown:

import random

from deap import base, creator, tools

Define the evaluation function. It is the first step to create a genetic algorithm.

def eval_func(individual):

target_sum = 15
return len(individual) - abs(sum(individual) - target_sum),

Now, create the toolbox with the right parameters:

def create_toolbox(num_bits):

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)

Initialize the toolbox:

toolbox = base.Toolbox()

toolbox.register("attr_bool", random.randint, 0, 1)

toolbox.register("individual", tools.initRepeat, creator.Individual,
toolbox.attr_bool, num_bits)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)

Register the evaluation operator:

toolbox.register("evaluate", eval_func)

Now, register the crossover operator:

toolbox.register("mate", tools.cxTwoPoint)

Register a mutation operator:

toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)

Define the operator for breeding:

toolbox.register("select", tools.selTournament, tournsize=3)
return toolbox
if __name__ == "__main__":
num_bits = 45
toolbox = create_toolbox(num_bits)
random.seed(7)
population = toolbox.population(n=500)
probab_crossing, probab_mutating = 0.5, 0.2
num_generations = 10
print('\nEvolution process starts')

Evaluate the entire population:

fitnesses = list(map(toolbox.evaluate, population))
for ind, fit in zip(population, fitnesses):
ind.fitness.values = fit
print('\nEvaluated', len(population), 'individuals')

Create and iterate through generations:

for g in range(num_generations):
print("\n- Generation", g)

Selecting the next generation individuals:

offspring = toolbox.select(population, len(population))

Now, clone the selected individuals:

offspring = list(map(toolbox.clone, offspring))

Apply crossover and mutation on the offspring:

for child1, child2 in zip(offspring[::2], offspring[1::2]):
if random.random() < probab_crossing:
toolbox.mate(child1, child2)

Delete the fitness value of child:

del child1.fitness.values
del child2.fitness.values

Now, apply mutation:

for mutant in offspring:
if random.random() < probab_mutating:
toolbox.mutate(mutant)
del mutant.fitness.values

Evaluate the individuals with an invalid fitness:

invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)

for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
print('Evaluated', len(invalid_ind), 'individuals')

Now, replace population with next generation individual:

population[:] = offspring

Print the statistics for the current generations:

fits = [ind.fitness.values[0] for ind in population]
length = len(population)
mean = sum(fits) / length

sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print('Min =', min(fits), ', Max =', max(fits))
print('Average =', round(mean, 2), ', Standard deviation =',
round(std, 2))
print("\n- Evolution ends")

Print the final output:

best_ind = tools.selBest(population, 1)[0]
print('\nBest individual:\n', best_ind)
print('\nNumber of ones:', sum(best_ind))

Following would be the output:

Evolution process starts
Evaluated 500 individuals
- Generation 0
Evaluated 295 individuals
Min = 32.0 , Max = 45.0
Average = 40.29 , Standard deviation = 2.61
- Generation 1
Evaluated 292 individuals
Min = 34.0 , Max = 45.0
Average = 42.35 , Standard deviation = 1.91
- Generation 2
Evaluated 277 individuals
Min = 37.0 , Max = 45.0
Average = 43.39 , Standard deviation = 1.46
… … … …
- Generation 9
Evaluated 299 individuals
Min = 40.0 , Max = 45.0
Average = 44.12 , Standard deviation = 1.11
- Evolution ends
Best individual:
[0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1]
Number of ones: 15