Classification and Regression Using Supervised Learning 4(Naïve Bayes classifier)

Naïve Bayes is a technique used to build classifiers using Bayes theorem. Bayes theorem describes the probability of an event occurring based on different conditions that are related to this event. We build a Naïve Bayes classifier by assigning class labels to problem instances. These problem instances are represented as vectors of feature values. The assumption here is that the value of any given feature is independent of the value of any other feature. This is called the independence assumption, which is the naïve part of a Naïve Bayes classifier.

Given the class variable, we can just see how a given feature affects, it regardless of its affect on other features. For example, an animal may be considered a cheetah if it is spotted, has four legs, has a tail, and runs at about 70 MPH. A Naïve Bayes classifier considers that each of these features contributes independently to the outcome. The outcome refers to the probability that this animal is a cheetah. We don't concern ourselves with the correlations that may exist between skin patterns, number of legs, presence of a tail, and movement speed. Let's see how to build a Naïve Bayes classifier through the program shown below:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_validate
from utilities import visualize_classifier

# Input file containing data
input_file = 'data_multivar_nb.txt'

# Load data from input file
data = np.loadtxt(input_file, delimiter=',')
X, y = data[:, :-1], data[:, -1]

# Create Naïve Bayes classifier
classifier = GaussianNB()

# Train the classifier
classifier.fit(X, y)

# Predict the values for training data
y_pred = classifier.predict(X)

# Compute accuracy
accuracy = 100.0 * (y == y_pred).sum() / X.shape[0]
print("Accuracy of Naïve Bayes classifier =", round(accuracy, 2), "%")
# Visualize the performance of the classifier
visualize_classifier(classifier, X, y)

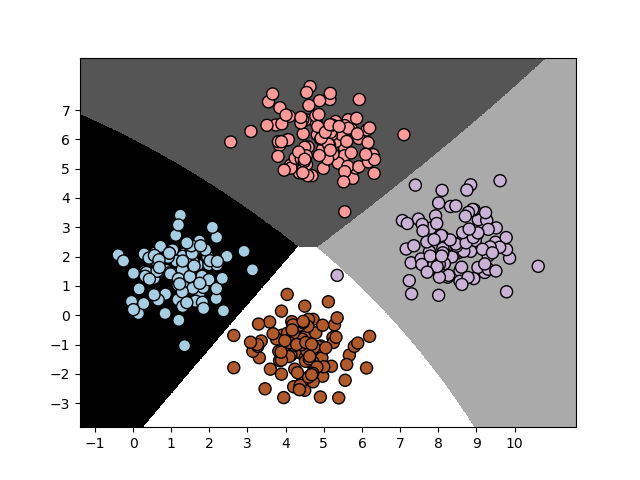
When we run the program we get the following output and graph:

Accuracy of Naïve Bayes classifier = 99.75 %

As usual or program starts with the necessary imports. Then we define the Input file containing data this file is data_multivar_nb.txt is used as the source of data. You can replace this with your own data source file. This file contains comma separated values in each line. Next we load the data from this file.

The we create an instance of the Naïve Bayes classifier. We used the Gaussian Naïve Bayes classifier here. In this type of classifier, we assume that the values associated in each class follow a Gaussian distribution. Next we train the classifier using the training data and then run the classifier on the training data and predicted the output.

We then computed the accuracy of the classifier by comparing the predicted values with the true labels, and then visualize the performance as shown in the graph.

The preceding method to compute the accuracy of the classifier is not very robust. We need to perform cross validation, so that we don't use the same training data when we are testing it. Split the data into training and testing subsets. As specified by the test_size parameter in the line below, we will allocate 80% for training and the remaining 20% for testing. We'll then train a Naïve Bayes classifier on this data. See the code below:

# Split data into training and test data
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=3)
classifier_new = GaussianNB()
classifier_new.fit(X_train, y_train)
y_test_pred = classifier_new.predict(X_test)

Now compute the accuracy of the classifier and visualize the performance. See the code below:

# compute accuracy of the classifier
accuracy = 100.0 * (y_test == y_test_pred).sum() / X_test.shape[0]
print("Accuracy of the new classifier =", round(accuracy, 2), "%")
# Visualize the performance of the classifier
visualize_classifier(classifier_new, X_test, y_test)

We'll use the inbuilt functions to calculate the accuracy, precision, and recall values based on threefold cross validation. See the code below:

num_folds = 3
accuracy_values = cross_val_score(classifier,
X, y, scoring='accuracy', cv=num_folds)
print("Accuracy: " + str(round(100*accuracy_values.mean(), 2)) + "%")
precision_values = cross_val_score(classifier,
X, y, scoring='precision_weighted', cv=num_folds)
print("Precision: " + str(round(100*precision_values.mean(), 2)) + "%")
recall_values = cross_val_score(classifier,
X, y, scoring='recall_weighted', cv=num_folds)
print("Recall: " + str(round(100*recall_values.mean(), 2)) + "%")
f1_values = cross_val_score(classifier,
X, y, scoring='f1_weighted', cv=num_folds)
print("F1: " + str(round(100*f1_values.mean(), 2)) + "%")


Now when we run the program we get the following output and graph:

The preceding output shows the boundaries obtained from the classifier. We can see that they separate the 4 clusters well and create regions with boundaries based on the distribution of the input datapoints. You will see in the following on terminal and graph as output, the second training run with cross validation:

Accuracy of Naïve Bayes classifier = 99.75 %
Accuracy of the new classifier = 100.0 %
Accuracy: 99.75%
Precision: 99.76%
Recall: 99.75%
F1: 99.75%
------------------
(program exited with code: 0)

Press any key to continue . . .