Supervised learning consists of learning possible patterns between two or more features reading values from a training set; the learning is possible because the training set contains known results (target or labels). All models in scikit-learn are referred to as supervised estimators, using the fit(x, y) function that makes their training.
x comprises the features observed, while y indicates the target. Once the estimator has carried out the training, it will be able to predict the value of y for any new observation x not labeled. This operation will make it through the predict(x) function.
Some classic examples of supervised learning are:
• Classification, using the Iris Dataset
• K-Nearest Neighbors Classifier
• Support Vector Machines (SVC)
• Regression, using the Diabetes Dataset
• Linear Regression
• Support Vector Machines (SVR)
Let's first discuss about The Iris Flower Dataset:
The Iris Flower Dataset is a particular dataset used for the first time by Sir Ronald Fisher in 1936. It is often also called Anderson Iris Dataset, after the person who collected the data directly measuring the size of the various parts of the iris flowers. In this dataset, data from three different species of iris (Iris silky, virginica Iris, and Iris versicolor) are collected and these data correspond to the length and width of the sepals and the length and width of the petals. The figure below shows the Iris versicolor and the petal and sepal width and length
This dataset is currently being used as a good example for many types of analysis, in particular for the problems of classification, which can be approached by means of machine learning methodologies. It is no coincidence then that this dataset is provided along with the scikit-learn library as a 150x4 NumPy array. To use the datasets we need to import them into our program:
from sklearn import datasets
Also we need to install scikit -learn using pip install -U scikit -learn. The following program will get an array of elements, the size of sepals and petals respectively:
from sklearn import datasets
iris = datasets.load_iris()
print(iris.data)
The output of the program is shown below:
2018-12-27 00:00:00
2018-12-27 16:29:00
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
:
:
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
------------------
(program exited with code: 0)
Press any key to continue . . .
As a result we get an array of 150 elements, each containing four numeric values: the size of sepals and petals respectively. Using the target attribute we can know what kind of flower belongs each item. To know the correspondence between the species and number, we have to call the target_names attribute. See the following program :
iris = datasets.load_iris()
print(iris.data)
print("\nWhat kind of flower belongs each item\n")
print(iris.target)
print("\nWhat kind of correspondence between the species and number\n")
print(iris.target_names)
The output of the program is shown below:
2018-12-27 00:00:00
2018-12-27 16:29:00
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
:
:
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
What kind of flower belongs each item
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
What kind of correspondence between the species and number
['setosa' 'versicolor' 'virginica']
------------------
(program exited with code: 0)
Press any key to continue . . .
We obtain 150 items with three possible integer values (0, 1, and 2), which correspond to the three species of iris.
Now to better understand this dataset we'll use the matplotlib library, using the techniques we learned in previous posts. We create a scatterplot that displays the three different species in three different colors. The x-axis will represent the length of the sepal while the y-axis will represent the width of the sepal. See the following program :
iris = datasets.load_iris()
print(iris.data)
x = iris.data[:,0] #X-Axis - sepal length
y = iris.data[:,1] #Y-Axis - sepal length
species = iris.target #Species
x_min, x_max = x.min() - .5,x.max() + .5
y_min, y_max = y.min() - .5,y.max() + .5
#SCATTERPLOT
plt.figure()
plt.title('Iris Dataset - Classification By Sepal Size')
plt.scatter(x,y, c=species)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
The output of the program is shown below which is the scatterplot:
The purple ones are the Iris setosa, flowers, green ones are the Iris versicolor, and yellow ones are the Iris virginica. We can see how the Iris setosa features differ from the other two, forming a cluster of blue dots separate from the others.
Now let's follow the same procedure, but this time using the other two variables, that is the measure of the length and width of the petal. See the following program :
iris = datasets.load_iris()
x = iris.data[:,2] #X-Axis - petal lenght
y = iris.data[:,3] #Y-Axis - petal width
species = iris.target #species
x_min, x_max = x.min() - .5, x.max() + .5
y_min, y_max = y.min() - .5, y.max() + .5
#SCATTERPLOT
plt.figure()
plt.title('Iris Dataset - Classification By Petal Sizes', size = 14)
plt.scatter(x,y, c=species)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
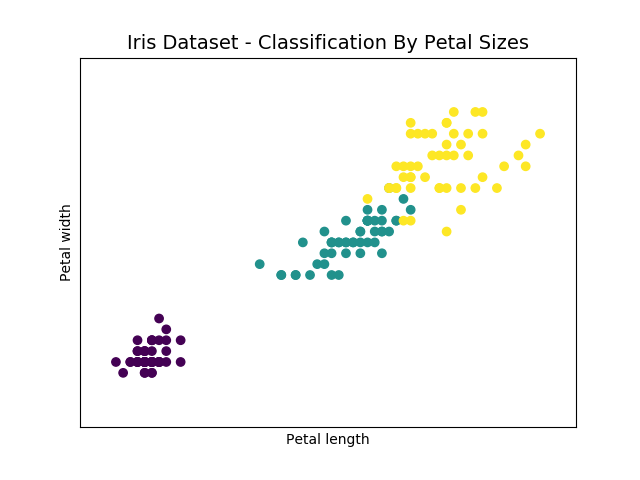
The output scatterplot is shown below:
In this case the division between the three species is much more evident. We have three different clusters. We represented two scatterplots, one for the petals and one for sepals, but how we can unify the whole thing? Four dimensions are a problem that even a Scatterplot 3D is not able to solve. In this regard a special technique called Principal Component Analysis (PCA) has been developed.
The PCA Decomposition
This technique allows to reduce the number of dimensions of a system keeping all the information for the characterization of the various points, the new dimensions generated are called principal components. In our case, we can reduce the system from four to three dimensions and then plot the results within a 3D scatterplot. In this way we can use measures both of sepals and of petals for
characterizing the various species of iris of the test elements in the dataset.
The scikit-learn function that allows us to do the dimensional reduction is the fit_transform() function. It belongs to the PCA object. In order to use it, first we need to import the PCA sklearn.decomposition module. Then we have to define the object constructor using PCA() and define the number of new dimensions (principal components) as a value of the n_components option. In our case, it is 3. Finally we have to call the fit_transform() function by passing the four-dimensional Iris Dataset as an argument. See the following program :
iris = datasets.load_iris()
#x = iris.data[:,1] #X-Axis - sepal width
#y = iris.data[:,2] #Y-Axis - petal lenght
species = iris.target #species
x_reduced = PCA(n_components=3).fit_transform(iris.data)
#SCATTERPLOT 3D
fig = plt.figure()
ax = Axes3D(fig)
ax.set_title('Iris Dataset by PCA', size = 14)
ax.scatter(x_reduced[:,0],x_reduced[:,1],x_reduced[:,2], c=species)
ax.set_xlabel('First eigenvector')
ax.set_ylabel('Second eigenvector')
ax.set_zlabel('Third eigenvector')
ax.w_xaxis.set_ticklabels(())
ax.w_yaxis.set_ticklabels(())
ax.w_zaxis.set_ticklabels(())
plt.show()
The output scatterplot is shown below:
In order to visualize the new values you will use a scatterplot 3D using the mpl_toolkits.mplot3d module of matplotlib. The three species of iris are well characterized with respect to each other to form a cluster.
Here I am ending today’s post. In the next post we will perform a classification using K-Nearest Neighbors Classifier. Until we meet again keep practicing and learning Python, as Python is easy to learn!
x comprises the features observed, while y indicates the target. Once the estimator has carried out the training, it will be able to predict the value of y for any new observation x not labeled. This operation will make it through the predict(x) function.
Some classic examples of supervised learning are:
• Classification, using the Iris Dataset
• K-Nearest Neighbors Classifier
• Support Vector Machines (SVC)
• Regression, using the Diabetes Dataset
• Linear Regression
• Support Vector Machines (SVR)
Let's first discuss about The Iris Flower Dataset:
The Iris Flower Dataset is a particular dataset used for the first time by Sir Ronald Fisher in 1936. It is often also called Anderson Iris Dataset, after the person who collected the data directly measuring the size of the various parts of the iris flowers. In this dataset, data from three different species of iris (Iris silky, virginica Iris, and Iris versicolor) are collected and these data correspond to the length and width of the sepals and the length and width of the petals. The figure below shows the Iris versicolor and the petal and sepal width and length
This dataset is currently being used as a good example for many types of analysis, in particular for the problems of classification, which can be approached by means of machine learning methodologies. It is no coincidence then that this dataset is provided along with the scikit-learn library as a 150x4 NumPy array. To use the datasets we need to import them into our program:
from sklearn import datasets
Also we need to install scikit -learn using pip install -U scikit -learn. The following program will get an array of elements, the size of sepals and petals respectively:
from sklearn import datasets
iris = datasets.load_iris()
print(iris.data)
The output of the program is shown below:
2018-12-27 00:00:00
2018-12-27 16:29:00
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
:
:
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
------------------
(program exited with code: 0)
Press any key to continue . . .
As a result we get an array of 150 elements, each containing four numeric values: the size of sepals and petals respectively. Using the target attribute we can know what kind of flower belongs each item. To know the correspondence between the species and number, we have to call the target_names attribute. See the following program :
iris = datasets.load_iris()
print(iris.data)
print("\nWhat kind of flower belongs each item\n")
print(iris.target)
print("\nWhat kind of correspondence between the species and number\n")
print(iris.target_names)
The output of the program is shown below:
2018-12-27 00:00:00
2018-12-27 16:29:00
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
:
:
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
What kind of flower belongs each item
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
What kind of correspondence between the species and number
['setosa' 'versicolor' 'virginica']
------------------
(program exited with code: 0)
Press any key to continue . . .
We obtain 150 items with three possible integer values (0, 1, and 2), which correspond to the three species of iris.
Now to better understand this dataset we'll use the matplotlib library, using the techniques we learned in previous posts. We create a scatterplot that displays the three different species in three different colors. The x-axis will represent the length of the sepal while the y-axis will represent the width of the sepal. See the following program :
iris = datasets.load_iris()
print(iris.data)
x = iris.data[:,0] #X-Axis - sepal length
y = iris.data[:,1] #Y-Axis - sepal length
species = iris.target #Species
x_min, x_max = x.min() - .5,x.max() + .5
y_min, y_max = y.min() - .5,y.max() + .5
#SCATTERPLOT
plt.figure()
plt.title('Iris Dataset - Classification By Sepal Size')
plt.scatter(x,y, c=species)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
The output of the program is shown below which is the scatterplot:
Now let's follow the same procedure, but this time using the other two variables, that is the measure of the length and width of the petal. See the following program :
iris = datasets.load_iris()
x = iris.data[:,2] #X-Axis - petal lenght
y = iris.data[:,3] #Y-Axis - petal width
species = iris.target #species
x_min, x_max = x.min() - .5, x.max() + .5
y_min, y_max = y.min() - .5, y.max() + .5
#SCATTERPLOT
plt.figure()
plt.title('Iris Dataset - Classification By Petal Sizes', size = 14)
plt.scatter(x,y, c=species)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
The output scatterplot is shown below:
The PCA Decomposition
This technique allows to reduce the number of dimensions of a system keeping all the information for the characterization of the various points, the new dimensions generated are called principal components. In our case, we can reduce the system from four to three dimensions and then plot the results within a 3D scatterplot. In this way we can use measures both of sepals and of petals for
characterizing the various species of iris of the test elements in the dataset.
The scikit-learn function that allows us to do the dimensional reduction is the fit_transform() function. It belongs to the PCA object. In order to use it, first we need to import the PCA sklearn.decomposition module. Then we have to define the object constructor using PCA() and define the number of new dimensions (principal components) as a value of the n_components option. In our case, it is 3. Finally we have to call the fit_transform() function by passing the four-dimensional Iris Dataset as an argument. See the following program :
iris = datasets.load_iris()
#x = iris.data[:,1] #X-Axis - sepal width
#y = iris.data[:,2] #Y-Axis - petal lenght
species = iris.target #species
x_reduced = PCA(n_components=3).fit_transform(iris.data)
#SCATTERPLOT 3D
fig = plt.figure()
ax = Axes3D(fig)
ax.set_title('Iris Dataset by PCA', size = 14)
ax.scatter(x_reduced[:,0],x_reduced[:,1],x_reduced[:,2], c=species)
ax.set_xlabel('First eigenvector')
ax.set_ylabel('Second eigenvector')
ax.set_zlabel('Third eigenvector')
ax.w_xaxis.set_ticklabels(())
ax.w_yaxis.set_ticklabels(())
ax.w_zaxis.set_ticklabels(())
plt.show()
The output scatterplot is shown below:
In order to visualize the new values you will use a scatterplot 3D using the mpl_toolkits.mplot3d module of matplotlib. The three species of iris are well characterized with respect to each other to form a cluster.
Here I am ending today’s post. In the next post we will perform a classification using K-Nearest Neighbors Classifier. Until we meet again keep practicing and learning Python, as Python is easy to learn!
0 comments:
Post a Comment